Major and Minor Intervals
Late Antiquity
The movement of a melodic line against an ison creates a rich harmonic texture, especially when compared to the monophonic unisonal singing that preceded it. This necessitates a more advanced form of harmonic analysis.
Intervals can now be grouped into different categories: perfect, major, and minor. It cannot be stressed enough that the generic interval (unison, second, third, fourth, fifth, sixth, seventh, octave) must be identified first, before identifying the harmonic quality (perfect, major, minor.) Many a music theory student has incorrectly named an interval by neglecting this first step.
That caveat in place, octaves, fifths, and fourths (the intervals naturally occurring as the first four tones of the harmonic series at frequency ratios of 1:2, 2:3, and 3:4) are known as perfect intervals.

By contrast, seconds, thirds, sixths, and sevenths, have both a major version and a minor version. In all cases, the major interval is one semitone higher than the minor interval.
A minor second is a second consisting of a single semitone.
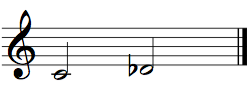
A major second is a second consisting of one whole tone.

A minor third is a third consisting of a one whole tone and one semitone.
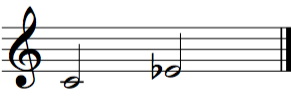
A major third is a third consisting of two whole tones.

A minor sixth is a sixth consisting of a perfect fifth plus one semitone.
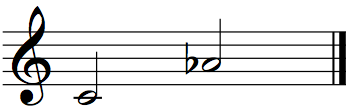
A major sixth is a third consisting of a perfect fifth plus one whole tone.

A minor seventh is a seventh one whole tone below the octave.

A major seventh is a seventh one semitone below the octave.

The table below shows you whether an interval is minor (m), major (M), or perfect (P) based on the number of semitones (row) and generic interval (column.)
| Unison | 2nd | 3rd | 4th | 5th | 6th | 7th | Octave | |
| 0 | P | |||||||
| 1 | m | |||||||
| 2 | M | |||||||
| 3 | m | |||||||
| 4 | M | |||||||
| 5 | P | |||||||
| 6 | ||||||||
| 7 | P | |||||||
| 8 | m | |||||||
| 9 | M | |||||||
| 10 | m | |||||||
| 11 | M | |||||||
| 12 | P |
